The Bohr energies for an electron orbiting a nucleus with charge
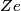 and mass and mass 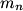 is is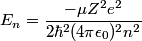 where 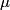 is the reduced mass of the electron and the nucleus. In this case is the reduced mass of the electron and the nucleus. In this case 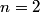 , , 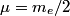 . Therefore, the energy is . Therefore, the energy is 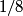 of the ground-state energy of hydrogen. Therefore, answer (E) is correct. of the ground-state energy of hydrogen. Therefore, answer (E) is correct. |